DSO总结

论文《Direct Sparse Odometry》的阅读笔记。

1. Calibration

DSO中结合了几何校正和光度校正两个模型，其中几何校正为小孔相机模型。

光度校正

光度成像模型为

$$I_i(x)=G(t_iV(\boldsymbol x)B_i(\boldsymbol x))$$

其中，$t_i$为曝光时间，$I_i(x)$为图像像素值，$G$为相机的响应函数，是相机的固有属性。$V$建模光学元件透镜的影响，即图像中心和边缘的亮度值不一致(vignetting)，如下图所示。$B_i$是辐照度(irradiance)，表示相机传感器接收到的入射光强。 <div align=center> </div> 因此对图像的光度校正模型为

$$I_i^{'}(x)=t_iB_i(x)=\frac{G^{-1}(I_i(x))}{V(x)}$$

该校正模型去除了vignetting的影响。（为什么最后不加上响应函数$G$？，即$I_i'(x)=G(t_iB_i(x))$）后文中的$I(x)$均指光度校正过的值。

几何校正和光度校正是怎么同时做的，先通过几何标定去除畸变，再给去除畸变的图像做光度标定？ 只要光度标定参数是在去除畸变的基础上得到的，几何标定和光度标定就不会相互影响。

2. 光度误差模型

对于host帧$i$中的点$\boldsymbol p$, 其在target帧$j$中的投影为$\boldsymbol p’$，则定义该点在这两帧中的光度误差为

$$\begin{equation} E_{\boldsymbol p_j}=\sum_{\boldsymbol p\in N_p}w_p||(I_j[\boldsymbol p']-b_j)-\frac{t_je^{a_j}}{t_ie^{a_i}}(I_i[\boldsymbol p]-b_i)||_\gamma \end{equation}$$

其中$w_p=\frac{c^2}{c^2+||\nabla I_i(\boldsymbol p)||_2^2}$为权重，像素的梯度越高，则其权重越小。减小噪声点的影响？

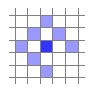
$N_p$表示residual pattern，如下图所示，在每个点周围选择7个点，忽略右下角点是为了使用SSE加速。因此每个点的光度误差是8个点的误差之和。 <div align=center> </div> 为了处理曝光时间未知的情况，添加了一个仿射亮度变换函数(affine brightness transfer function)$e^{-a_i}(I_i-b_i)$。（通过该函数来大致拟合成像过程，从而消除光度误差, $e^{-a}$用于校正曝光时间、$b_i$用于校正图像亮度基底的影响[5]）

对于未进行光度标定的图像，则$G=V=t=1$，即$I_i^{‘}(x)=I_i(x)$。
对于已进行光度标定的图像，$a,b$为0或很小的数，因此上式等价于

$$E_{\boldsymbol p_j}=\sum_{\boldsymbol p\in N_p}w_p||I_j[\boldsymbol p']-\frac{t_j}{t_i}I_i[\boldsymbol p]||_\gamma$$

则最终计算的是两张图像之间的辐照度($B$)的误差。 总的光度误差为

$$\begin{equation} E_{photo}=\sum_{i\in F}\sum_{\boldsymbol p\in P_i}\sum_{j\in obs(\boldsymbol p)}E_{\boldsymbol p_j} \end{equation}$$

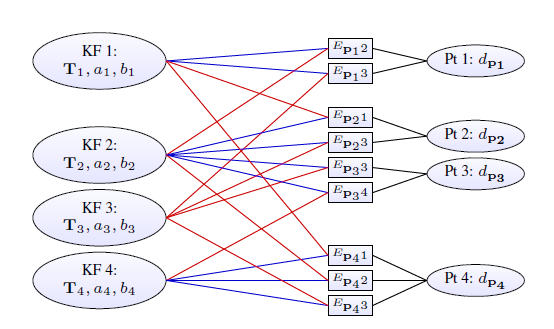
其中，$F$表示所有帧(key frame还是active frame还是所有普通的frame？)的集合，$P_i$表示帧$F_i$中的所有点(candidate point？active point?)，$obs(\boldsymbol p)$表示所有观测到$\boldsymbol p$点的其他帧。后续通过滑动窗口最小化该误差值，则$F$是滑动窗口内的所有帧，盲猜帧和点都是active。
最终构建的因子图如下所示：
<div align=center> </div> 在曝光时间已知并且已进行光度标定的情况下，还会加入一个正则项用来约束$a,b$的大小(此时$a,b$的作用已由光度标定完成)：

$$E_{prior}=\sum_{i\in F}(\lambda_aa_i^2+\lambda_bb_i^2)$$

3. Windowed Optimization & Marginalization

滑动窗口优化使用GN方法，则

$$\boldsymbol H =\boldsymbol{J}^T\boldsymbol{WJ} \\ \boldsymbol b = -\boldsymbol{J}^T\boldsymbol{Wr}$$

$\boldsymbol W$是权重矩阵（怎么得到的？）（公式1中的$w_p$），$\boldsymbol J$的推导见下一节。
$\boldsymbol J_k$的形式为

$$\begin{align} \boldsymbol{J}_k &= \frac{\partial r_k((\boldsymbol{\delta}+\boldsymbol{x})\boxplus\boldsymbol{\zeta}_0)}{\partial \boldsymbol{\delta}} \\ &= \left[ \begin{matrix} \underbrace{\frac{\partial I_j}{\partial \boldsymbol p'}}_{\boldsymbol J_I}\underbrace{\frac{\partial \boldsymbol p'((\boldsymbol{\delta}+\boldsymbol{x})\boxplus\boldsymbol{\zeta}_0)}{\partial \boldsymbol \delta_{geo}}}_{\boldsymbol J_{geo}},\end{matrix} \begin{matrix} \underbrace{\frac{\partial r_k((\boldsymbol{\delta}+\boldsymbol{x})\boxplus\boldsymbol{\zeta}_0)}{\partial \boldsymbol \delta_{photo}}}_{\boldsymbol J_{photo}} \end{matrix} \right] \end{align}$$ （太难看了，怎么把大括号放矩阵外面？）

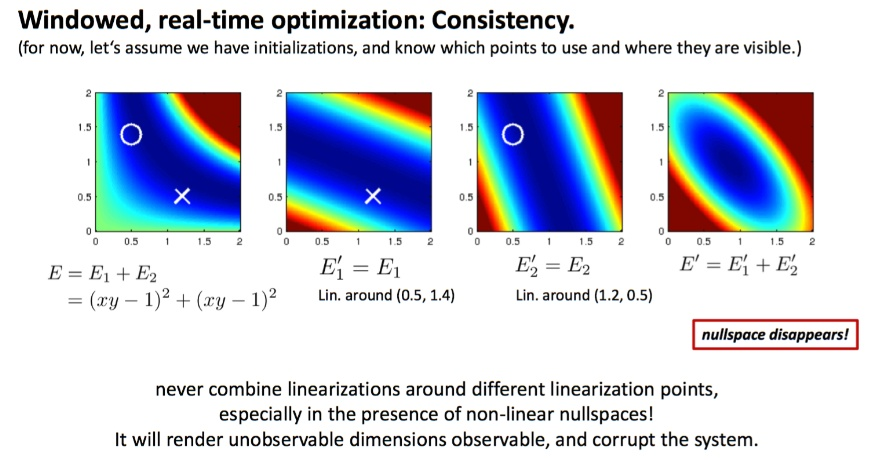
使用滑动窗口时，为了减小计算量，需要将部分变量移出窗口，若是直接丢掉这些变量，则会破坏原有的约束关系，损失约束信息，因此需要使用边缘化，将约束信息转化为待优化变量的先验分布，实际上是一个从联合概率密度分布获得边缘概率密度分布的过程[6]。被边缘化的变量可能和剩余的变量之间有约束，因此若直接丢弃该变量，则约束也被舍弃了，在后续的优化过程中势必会破坏该约束，而边缘化是将该约束信息转换为剩余变量的先验信息[7]。也是由于该先验信息的存在而需要使用FEJ策略已保持一致性。例如，当前优化状态量为$[x, y]$，需要边缘化$x$，此时$y$在$(x_0, y_0)$处线性化，则得到一个先验的Hessian矩阵$H_0$，此时新加入变量$z$，则优化变量变为$[y,z]$，但是此时$y$已经更新，因此再次优化的时候会在$(y_1,z_0)$处进行线性化，得到新的Hessian矩阵$H_1$，则求解的增量方程变为$(H_0+H_1)x=b$[10]。所以$z$是在$(y_1,z_0)$处线性化，而由于先验$H$的存在，$y$不是在该点线性化，因此导致不一致性的问题？但是用了FEJ以后$y$和$z$仍然不是在同一点线性化的。不同的线性化点并不是相对于不同的变量而言的，而是指函数两次线性化时的点（变量的值）是相同的，若在不同的点线性化两次后的加和就可能导致零空间的降维。如下图所示，$E_1$和$E_2$在不同的点线性化后使原函数的零空间消失。

EFJ如何解决这个问题？ $H_0$只包含先验信息，因此只有在上一次边缘化时增加了先验的变量才有值，其余均为0，所以加上$H_0$不会对其他变量有影响，因此下一次优化时，只需这些变量在初始值处线性化即可，迭代过程不更新，优化完成后再更新。

<div align=center> </div>

误差函数$r_k$中存在非线性零空间(nullspace)（即该变量的变化不会影响$r_k$的变化，DSO中是尺度和绝对位姿），因此若在不同的点对这些变量进行线性化，则会导致零空间的降维，相当于引入了错误的信息，使不可观状态量变得可观了。为了解决这个问题，需要对这些不可观变量同时进行线性化，即First Estimate Jacobians，$\boldsymbol J_{geo},\boldsymbol J_{photo}$均在$\boldsymbol \xi_0$处进行计算，每次迭代时只更新$x$，一次优化完成后更新$\xi_0$。$\boldsymbol J_{geo},\boldsymbol J_{photo}$是足够光滑的，因此实际使用中，效果很好。

边缘化某一帧时，首先边缘化该帧中的所有active point以及所有最近两帧中未观测到的点，该帧的active point在其他帧中的observation直接丢弃（怎么直接丢弃？直接将$H$中对应的行列置为0？）（直接置为0。）

问题：

1. 只在一次优化的6次迭代中使用FEJ，下次优化时会重新计算Jacobian矩阵？
2. 先验Hessian矩阵$H$是一个单独的矩阵？$H$会在整个程序运行期间一直维护，每次进行边缘化的时候进行累加？还是只保留最新的？
3. 边缘化旧的状态量，添加新的状态量和优化的时机？创建了新的关键帧后，需要边缘化旧的，优化怎么进行？进行一次优化，前几次迭代边缘化，后几次迭代优化新加入的状态？（错，一次迭代中的$H$是不变的？！）或一次优化中不考虑新加入的变量，只是边缘掉旧的状态量，更新剩余变量后直接把新加入的状态量加入到窗口中，而不进行优化，下一次边缘化的时候再优化？（感觉也不太可能）或者进行两次优化，第一次边缘化，第二次优化新变量？
4. 不同的线性化点是如何出现的？
5. 先验Hessian矩阵怎么计算的？

4. Jacobian矩阵推导

残差公式为：

$$\begin{equation} r_k = (I_j[\boldsymbol p'(\boldsymbol T_i,\boldsymbol T_j,d,\boldsymbol{c})]-b_j)-\frac{t_je^{a_j}}{t_ie^{a_i}}(I_i[p]-b_i) \end{equation}$$

下标$i$表示host frame, $j$表示target frame。
则

$$\begin{align} \boldsymbol{J}_k &= \frac{\partial r_k((\boldsymbol{\delta}+\boldsymbol{x})\boxplus\boldsymbol{\zeta}_0)}{\partial \boldsymbol{\delta}} \\ &= \left[ \begin{matrix} \frac{\partial I_j}{\partial \boldsymbol p'}\frac{\partial \boldsymbol p'((\boldsymbol{\delta}+\boldsymbol{x})\boxplus\boldsymbol{\zeta}_0)}{\partial \boldsymbol \delta_{geo}}, \frac{\partial r_k((\boldsymbol{\delta}+\boldsymbol{x})\boxplus\boldsymbol{\zeta}_0)}{\partial \boldsymbol \delta_{photo}} \end{matrix} \right] \end{align}$$

其中，$\boldsymbol \delta$包括两部分，$\boldsymbol \delta_{geo}$：几何参数（$\boldsymbol T_i, \boldsymbol T_j, d, \boldsymbol{c}$）和$\boldsymbol \delta_{photo}$:光度参数（$a_i,a_j,b_i,b_j$）。

4.0 图像梯度

$$ \begin{equation} \frac{\partial I_j}{\partial \boldsymbol p'}=[I_u, I_v,0] \end{equation} $$

$I_u,I_v$分别表示图像在$u,v$方向的梯度。

4.1 光度参数（$a_i,a_j,b_i,b_j$）

光度参数直接求导即可。

$$ \begin{align} \frac{\partial r_k}{\partial a_i} &= \frac{t_je^{a_j}}{t_ie^{a_i}}(I_i[\boldsymbol p]-b_i) \\ \frac{\partial r_k}{\partial a_j} &= -\frac{t_je^{a_j}}{t_ie^{a_i}}(I_i[\boldsymbol p]-b_i) \\ \frac{\partial r_k}{\partial b_i} &= \frac{t_je^{a_j}}{t_ie^{a_i}} \\ \frac{\partial r_k}{\partial b_j} &= -1 \end{align} $$

4.2 几何参数（$\boldsymbol T_i, \boldsymbol T_j, d, \boldsymbol c$）

4.2.1 对$\boldsymbol T_j,\boldsymbol T_i$的偏导

假设host frame中的一个像素点为$\boldsymbol p=[u_i, v_i, 1]^T$，深度为$d_i$, 记$\rho_i=1/d_i$。该点在target frame中的投影为

$$\begin{align} \rho_j^{-1}\boldsymbol p' &= \underbrace{\boldsymbol K \boldsymbol T_{j}\boldsymbol T_{i}^{-1}}_{\boldsymbol T_{ji}}\underbrace{\boldsymbol K^{-1}\rho_i^{-1}\boldsymbol p}_{\boldsymbol P_i} \\ &= \boldsymbol{KT}_{ji}\boldsymbol P_i \\ &= \boldsymbol K(\boldsymbol R_{ji}\boldsymbol P_i+\boldsymbol t_{ji}) \end{align}$$

$\boldsymbol P_i = [X_i, Y_i, Z_i]$为该点在host坐标系下的空间坐标。
$\boldsymbol P_j = [X_j, Y_j, Z_j]$为该点在frame坐标系下的空间坐标。

$\boldsymbol T_i, \boldsymbol T_j$的李代数表示分别为$\boldsymbol \xi_{i}，\boldsymbol \xi_{j}$。

由[1] P163-164可知：

$$ \begin{equation} \frac{\partial \boldsymbol p'}{\partial \boldsymbol \xi_j} = \left[ \begin{matrix} f_x\frac{1}{Z_j} & 0 & -f_x\frac{X_j}{Z_j^2} & -f_x\frac{X_jY_j}{Z_j^2} & f_x+f_x\frac{X_j^2}{Z_j^2} & -f_x\frac{Y_j}{Z_j} \\ 0 & f_y\frac{1}{Z_j} & -f_y\frac{Y_j}{Z_j^2} & -f_y-f_y\frac{Y_j^2}{Z_j^2} & f_y\frac{X_jY_j}{Z_j^2} & f_y\frac{Y_j}{Z_j} \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix} \right] \label{part_p_tj} \end{equation} $$

此处需要注意，[1]中$\frac{\partial\mathbf{TP}}{\partial\mathbf\xi}$中$\mathbf T$是相对于世界坐标系的绝对位姿，而本文中$\mathbf p’=\rho_j\mathbf{K}\mathbf T_{ji}\mathbf P_i$中的$\mathbf T_{ji}$是相对位姿。
可以通过如下变换将相对位姿变换矩阵变为绝对变换矩阵。

$$\begin{align*} \mathbf p' &= \rho_j\mathbf{KT}_{j}\mathbf T_i^{-1}\mathbf P_i \\ &= \rho_j\mathbf{KT}_{j}\mathbf P_w \end{align*}$$

或者利用[3]中的结论：

$$\begin{align} \frac{\partial\boldsymbol p'}{\partial\mathbf\xi_j} &= \frac{\partial\rho_j\mathbf{KT}_{ji}\mathbf P_i}{\partial\mathbf\xi_j} \\ &= \underbrace{\frac{\partial\rho_j\mathbf{KT}_{ji}\mathbf P_i}{\partial\mathbf\xi_{ji}}}_{1}\underbrace{\frac{\partial\mathbf\xi_{ji}}{\partial\mathbf\xi_{j}}}_{2} \\ \end{align}$$

这里省略了其次坐标到非齐次坐标的转换。上式中1为对绝对位姿的偏导，结果为\ref{part_p_tj}，根据[3]中结论$\frac{\partial\boldsymbol{\xi}_{ji}}{\partial\boldsymbol\xi_j}=\boldsymbol I$，即2为单位阵$\boldsymbol I$，因此可以得到式\ref{part_p_tj}。

同样由[3]，已知

$$\frac{\partial\boldsymbol{\xi}_{ji}}{\partial\boldsymbol\xi_i}=-\boldsymbol{Ad}_{\boldsymbol T_{ji}} \\ \boldsymbol{Ad}_{\boldsymbol T_{ji}}= \left[ \begin{matrix} \boldsymbol R_{ji} & \boldsymbol{t_{ji}^\wedge R_{ji}} \\ \boldsymbol 0 & \boldsymbol R_{ji} \end{matrix} \right]$$

所以

$$ \begin{align} \frac{\partial\boldsymbol p'}{\partial\boldsymbol\xi_i} &= \frac{\partial\rho_j\boldsymbol{KT}_{ji}\boldsymbol P_i}{\partial\boldsymbol\xi_i} \\ &= \frac{\partial\rho_j\boldsymbol{KT}_{ji}\boldsymbol P_i}{\partial\boldsymbol\xi_{ji}}\frac{\partial\boldsymbol\xi_{ji}}{\partial\boldsymbol\xi_{i}} \\ &= - \left[ \begin{matrix} f_x\frac{1}{Z_j} & 0 & -f_x\frac{X_j}{Z_j^2} & -f_x\frac{X_jY_j}{Z_j^2} & f_x+f_x\frac{X_j^2}{Z_j^2} & -f_x\frac{Y_j}{Z_j} \\ 0 & f_y\frac{1}{Z_j} & -f_y\frac{Y_j}{Z_j^2} & -f_y-f_y\frac{Y_j^2}{Z_j^2} & f_y\frac{X_jY_j}{Z_j^2} & f_y\frac{Y_j}{Z_j} \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix} \right] \left[ \begin{matrix} \boldsymbol R_{ji} & \boldsymbol{t_{ji}^\wedge R_{ji}} \\ \boldsymbol 0 & \boldsymbol R_{ji} \end{matrix} \right] \end{align} $$

4.2.2 对逆深度的导数

定义

$$\begin{equation} \boldsymbol p'=[u_j, v_j, 1]=\boldsymbol K[u, v, 1]^T=\rho_j\boldsymbol K(\boldsymbol R_{ji}\boldsymbol P_i+\boldsymbol t_{ji}) \label{p_asp} \end{equation}$$

其中$[u, v, 1]^T$为归一化平面的坐标，则有：

$$\begin{align} \frac{\partial \boldsymbol p'}{\partial \rho_i}&= \left[ \begin{matrix} \frac{\partial u_j}{\partial \rho_i} & \frac{\partial v_j}{\partial \rho_i} & 0 \end{matrix} \right]^T \\ &=\left[ \begin{matrix} \frac{\partial u_j}{\partial u}\cdot\frac{\partial u}{\partial \rho_i} & \frac{\partial v_j}{\partial v}\cdot\frac{\partial v}{\partial \rho_i} & 0 \end{matrix} \right]^T \end{align}$$

且

$$\begin{align} [u,v,1]^T&=\rho_j(\boldsymbol R_{ji}\boldsymbol P_i+\boldsymbol t_{ji}) \\ &=\rho_j(\boldsymbol R_{ji}\boldsymbol K^{-1}\rho_i^{-1}\boldsymbol p+\boldsymbol t_{ji}) \end{align}$$

记$\boldsymbol a=\boldsymbol R_{ji}\boldsymbol K^{-1}\boldsymbol p$，则

$$\begin{equation} [u,v,1]^T=\rho_j(\rho_i^{-1}\boldsymbol a+\boldsymbol t_{ji}) \end{equation}$$

即

$$\begin{equation} \left\{ \begin{aligned} u &= \rho_j(\rho_i^{-1}\boldsymbol a^1+\boldsymbol t_{ji}^1) \\ v &= \rho_j(\rho_i^{-1}\boldsymbol a^2+\boldsymbol t_{ji}^2) \\ 1 &= \rho_j(\rho_i^{-1}\boldsymbol a^3+\boldsymbol t_{ji}^3)\end{aligned} \right. \label{u_v_1} \end{equation}$$

其中，$\boldsymbol{a,t}$的上标$i$表示取第$i$行。消去$\rho_j$，则

$$\begin{equation} u = \frac{u}{1} = \frac{\rho_j(\rho_i^{-1}\boldsymbol a^1+\boldsymbol t_{ji}^1)}{\rho_j(\rho_i^{-1}\boldsymbol a^3+\boldsymbol t_{ji}^3)} = \frac{\boldsymbol a^1+\rho_i\boldsymbol t_{ji}^1}{\boldsymbol a^3+\rho_i\boldsymbol t_{ji}^3} \label{u} \end{equation}$$ $$\begin{align} \frac{\partial u}{\partial\rho_i}&=\frac{\boldsymbol t_{ji}^1(\boldsymbol a^3+\rho_i\boldsymbol t_{ji}^3)-\boldsymbol t_{ji}^3(\boldsymbol a^1+\rho_i\boldsymbol t_{ji}^1)}{(\boldsymbol a^3+\rho_i\boldsymbol t_{ji}^3)^2} \\ &=\frac{\boldsymbol t_{ji}^1-u\boldsymbol t_{ji}^3}{\boldsymbol a^3+\rho_i\boldsymbol t_{ji}^3} \\ &=(\boldsymbol t_{ji}^1-u\boldsymbol t_{ji}^3)\frac{\rho_j}{\rho_i} \end{align}$$

其中，第三个等号由公式\ref{u_v_1}的3式而来。
同理

$$\begin{equation} \frac{\partial v}{\partial\rho_i}=(\boldsymbol t_{ji}^2-u\boldsymbol t_{ji}^3)\frac{\rho_j}{\rho_i} \end{equation}$$

由公式\ref{p_asp}可得：

$$\begin{equation} \left[ \begin{matrix} u_j \\ v_j \\ 1 \end{matrix} \right]= \left[ \begin{matrix} f_xu+c_x \\ f_yv+c_y \\ 1 \end{matrix} \right] , \left[ \begin{matrix} \frac{\partial u_j}{\partial u} \\ \frac{\partial v_j}{\partial v} \end{matrix} \right]= \left[ \begin{matrix} f_x \\ f_y \end{matrix} \right] \label{part_u_j_u} \end{equation}$$

所以

$$ \begin{align} \frac{\partial \boldsymbol p'}{\partial \rho_i} &=\left[ \begin{matrix} \frac{\partial u_j}{\partial u}\cdot\frac{\partial u}{\partial \rho_i} \\ \frac{\partial v_j}{\partial v}\cdot\frac{\partial v}{\partial \rho_i} \\ 0 \end{matrix} \right] \\ &= \left[ \begin{matrix} f_x(\boldsymbol t_{ji}^1-u\boldsymbol t_{ji}^3)\frac{\rho_j}{\rho_i} \\ f_y(\boldsymbol t_{ji}^2-u\boldsymbol t_{ji}^3)\frac{\rho_j}{\rho_i} \\ 0 \end{matrix} \right] \end{align} $$

通过式\ref{u_v_1}消去$\rho_i$，则

$\begin{equation*} \frac{u-\rho_j\boldsymbol t_{ji}^1}{1-\rho_j\boldsymbol t_{ji}^3}=\frac{\boldsymbol a^1}{\boldsymbol a^3} \\ u = \frac{\boldsymbol a^1}{\boldsymbol a^3}+(\boldsymbol t_{ji}^1-\frac{\boldsymbol a^1}{\boldsymbol a^3}\boldsymbol t_{ji}^3)\rho_j \\ \end{equation*}$$\begin{align} \frac{\partial u}{\partial\rho_j} &= \boldsymbol t_{ji}^1-\frac{\boldsymbol a^1}{\boldsymbol a^3}\boldsymbol t_{ji}^3 \\ &= (\boldsymbol t_{ji}^1-u\boldsymbol t_{ji}^3)\frac{1}{1-\rho_j\boldsymbol t_{ji}^3} \end{align}$

同理

$$\frac{\partial v}{\partial\rho_j} = (\boldsymbol t_{ji}^2-v\boldsymbol t_{ji}^3)\frac{1}{1-\rho_j\boldsymbol t_{ji}^3}$$

所以

$$ \begin{align} \frac{\partial \boldsymbol p'}{\partial \rho_j} &=\left[ \begin{matrix} \frac{\partial u_j}{\partial u}\cdot\frac{\partial u}{\partial \rho_j} \\ \frac{\partial v_j}{\partial v}\cdot\frac{\partial v}{\partial \rho_j} \\ 0 \end{matrix} \right] \\ &= \left[ \begin{matrix} f_x(\boldsymbol t_{ji}^1-u\boldsymbol t_{ji}^3)\frac{1}{1-\rho_j\boldsymbol t_{ji}^3} \\ f_y(\boldsymbol t_{ji}^2-u\boldsymbol t_{ji}^3)\frac{1}{1-\rho_j\boldsymbol t_{ji}^3} \\ 0 \end{matrix} \right] \end{align} $$

4.2.3 对内参的偏导

对$f_x, f_y$：

$$\begin{equation} \boldsymbol p'= \left[ \begin{matrix} f_xu+c_x \\ f_yv+c_y \\ 1 \end{matrix} \right] \end{equation}$$

易得$\frac{\partial v}{\partial f_x}=0$, 所以

$$\begin{equation} \frac{\partial \boldsymbol p'}{\partial f_x}= \left[ \begin{matrix} u+f_x\frac{\partial u}{\partial f_x}\\ 0 \\ 0 \end{matrix} \right]= \left[ \begin{matrix} u+f_x\frac{\partial u}{\partial\boldsymbol P_i^T}\frac{\partial\boldsymbol P_i}{\partial\boldsymbol f_x}\\ 0 \\ 0 \end{matrix} \right] \end{equation}$$

由式\ref{u}可知

$$u = \frac{\rho_i^{-1}\boldsymbol r_1\overbrace{\boldsymbol K^{-1}\boldsymbol p}^{\boldsymbol P_i}+t_1}{\rho_i^{-1}\boldsymbol r_3\boldsymbol K^{-1}\boldsymbol p+t_3}=\frac{\rho_i^{-1}\boldsymbol r_1\boldsymbol P_i+t_1}{\rho_i^{-1}\boldsymbol r_3\boldsymbol P_i+t_3}$$

其中$\boldsymbol r_1=\boldsymbol R_{ji}^1, t_1=\boldsymbol t_{ji}^1,\boldsymbol r_3=\boldsymbol R_{ji}^3, t_3=\boldsymbol t_{ji}^3$，则

$$\begin{equation} \frac{\partial u}{\partial\boldsymbol P_i^T}= \left( \frac{\rho_i^{-1}(\boldsymbol r_1-u\boldsymbol r_3)}{\rho_i^{-1}\boldsymbol r_3\boldsymbol P_i+t_3} \right)^T=\frac{\rho_j}{\rho_i}(\boldsymbol r_1^T-u\boldsymbol r_3^T) \end{equation}$$ $$\boldsymbol P_i= \boldsymbol K^{-1}\boldsymbol p= \left[ \begin{matrix} f_x^{-1} & 0 & -f_x^{-1}c_x \\ 0 & f_y^{-1} & -f_y^{-1}c_y \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} u_i \\ v_i \\ 1 \end{matrix} \right]= \left[ \begin{matrix} f_x^{-1}u_i-f_x^{-1}c_x \\ f_y^{-1}v_i-f_y^{-1}c_y \\ 1 \end{matrix} \right] \\ $$ $$\begin{equation} \frac{\partial \boldsymbol P_i'}{\partial f_x}= \left[ \begin{matrix} -f_x^{-2}(u_i-c_x) \\ 0 \\ 0 \end{matrix} \right]= \left[ \begin{matrix} -uf_x^{-1} \\ 0 \\ 0 \end{matrix} \right] \end{equation}$$

所以

$$ \begin{align} \frac{\partial u}{\partial f_x}&=-\frac{\rho_j}{\rho_i}(r_{11}-ur_{31})uf_x^{-1} \\ \frac{\partial \boldsymbol p'}{\partial f_x}&= \left[ \begin{matrix} u-u\frac{\rho_j}{\rho_i}(r_{11}-ur_{31}) \\ 0 \\ 0 \end{matrix} \right] \end{align} $$

同理可得

$$ \begin{equation} \frac{\partial \boldsymbol p'}{\partial f_y}= \left[ \begin{matrix} 0 \\ v-v\frac{\rho_j}{\rho_i}(r_{21}-vr_{31}) \\ 0 \end{matrix} \right] \end{equation} $$

对$c_x, c_y$：

$$\begin{equation} \frac{\partial \boldsymbol p'}{\partial c_x}= \left[ \begin{matrix} 1+f_x\frac{\partial u}{\partial c_x}\\ 0 \\ 0 \end{matrix} \right]= \left[ \begin{matrix} 1+f_x\frac{\partial u}{\partial\boldsymbol P_i^T}\frac{\partial\boldsymbol P_i}{\partial\boldsymbol c_x}\\ 0 \\ 0 \end{matrix} \right] \\ \frac{\partial \boldsymbol P_i}{\partial c_x}= \left[ \begin{matrix} -f_x^{-1} \\ 0 \\ 0 \end{matrix} \right] \\ \end{equation}$$

所以

$$ \begin{equation} \frac{\partial \boldsymbol p'}{\partial c_x}= \left[ \begin{matrix} 1-\frac{\rho_j}{\rho_i}(r_{11}-ur_{31})\\ 0 \\ 0 \end{matrix} \right] \end{equation} $$

同理可得

$$ \begin{equation} \frac{\partial \boldsymbol p'}{\partial c_y}= \left[ \begin{matrix} 0 \\ 1-\frac{\rho_j}{\rho_i}(r_{21}-ur_{31})\\ 0 \end{matrix} \right] \end{equation} $$

5. Visual Odomtery Front-end

前端负责帧和点的管理（选取及边缘化，移除outlier及遮挡点），并且为新加入的变量提供优化初值。

5.1 帧管理

滑动窗口中总是保持7个active frame，新来的帧将根据这些active frame进行tracking，然后决定该帧是否成为一个关键帧，若否，则丢弃该帧，否则优化光度误差，最后边缘化其他帧。

1. Frame tracking 新关键帧创建后，将其他active frame中的active point全部投影到最新关键帧，新来的frame只需根据这一帧进行tracking，初始值根据匀速运动模型和图像金字塔（图像金字塔的作用？）得到，若tracking失败，则在27个不同的方向重新初始化（？）。
2. 关键帧的选择 策略：首先尽可能多的创建关键帧，然后再边缘化掉。 选取准则：
   1. 视角变换大
   2. 平移较大
   3. 曝光时间变化大 最终通过这三个准则的加权分数决定是否创建新的关键帧。
3. 关键帧的边缘化
   1. 最新两帧一定保留。
   2. 某一帧中的active point中少于5%被最新的active frame观测到，则边缘化该帧。
   3. 边缘化掉离最新关键帧远，但离其他关键帧近的关键帧。

5.2 点管理

总的active point为2000个，使他们尽可能在整个空间及active frame上均匀分布。首先在每个新的关键帧上选择2000个候选点，并且通过后续的tracking得到初始深度值，然后选择部分候选点成为active point。

1. 候选点的选择 尽可能选择在图像中分布均匀，并且梯度较大的点。
2. 候选点的tracking 沿极线搜索，最小化光度误差得到深度值和associated variance（？）。
3. 候选点激活 将所有active point投影到新的关键帧上，选择与已存在的active point距离最大的点激活（具体策略？与一个点还是所有点距离之和？）。

[8]推导了如何从多元高斯分布联合盖概率密度$p(a,b)$得到部分变量的条件概率密度$p(a|b)$。 [9]说明了多元高斯分布中协方差矩阵的逆$\sum^{-1}$等于Hessian矩阵$H$。

参考

1. 高翔, 张涛, 刘毅, 颜沁睿, 视觉SLAM十四讲：从理论与实践,电子工业出版社, 2017
2. DSO详解
3. Adjoint of SE(3)
4. 闲话矩阵求导
5. DSO之光度标定
6. 滑窗优化、边缘化、舒尔补、FEJ及fill-in问题
7. DSO 中的Windowed Optimization
8. Conditional and marginal distributions of a multivariate Gaussian
9. Relationship between the Hessian and Covariance Matrix for Gaussian Random Variables
10. 如何理解EKF中的consistency？ - jing胖的回答

---

• Previous
  ubuntu16.04下同步code-server与vscode的配置
• Next
  precision与accuracy的区别